Hur högt är bordet? Uppgiften för grundskoleelever i Kina kommer att utmana dig
Då och då dyker det upp matematiska gåtor på webben som sätter många människor i kris. Trots svårigheten börjar många entusiaster så fort de ser problemet att fundera på hur de ska lösa det. Många tar dessa tester som riktiga utmaningar mot sig själva , de slösar ingen tid utan beväpnar sig direkt med papper och penna, skriver ner problemet och börjar fundera, gör alla möjliga beräkningar tills glödlampan tänds och från det ögonblicket blir det lättare. Allt som krävs är rätt intuition.
Så fort många sett detta logiska matatematiska problem på webben, som föreslagits för grundskoleklasser i Kina, har de inte slösat någon tid utan försökt lösa det.
De bästa eleverna i grundskoleklasserna misslyckades dock. Faktum är att det inte är en lätt uppgift, endast ett fåtal personer har kommit fram till det rätta resultatet.
Tror du att du kan lösa det?
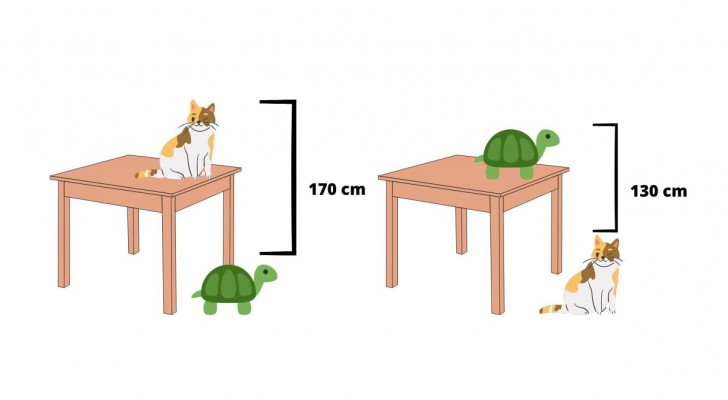
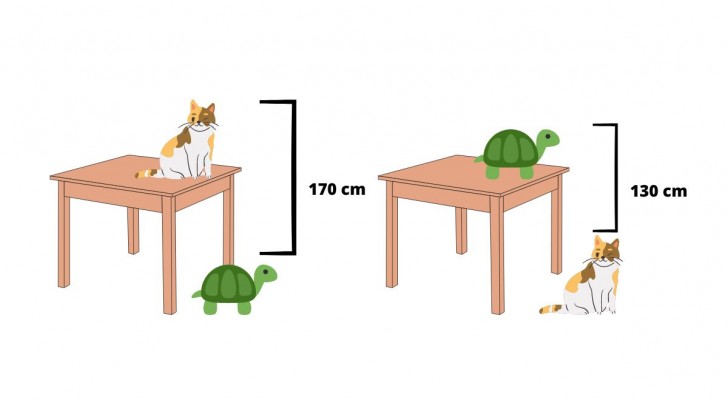
Rubriken på problemet lyder: beräkna höjden på bordet, med vetskap om att avståndet mellan kattens huvud och sköldpaddan på golvet är 170 cm, medan avståndet mellan sköldpaddans huvud på bordet och kattens huvud på golvet är 130 cm".
Alla som har försökt har gett sin egen tolkning av problemet och trott att de har hittat lösningen. Dessa resultat var dock inget annat än spekulationer. Av dessa skäl har experter vågat sig på detta test för att ge en tydlig förklaring, för att göra alla medvetna om uträkningen. Man kan använda sig av två typer av resonemang: ett algebraiskt och ett visuellt.
Algebraisk metod

Algebraisk metod: båda figurerna kan omvandlas till ekvationer. Den första blir:
h.katt+h.bord-sköldpadda=170 (h. står för höjd).
Den andra kan dock transkriberas som:
h.sköldpadda+h.bord-h.katt=130
I algebra kan två ekvationer adderas: givet att h.katt och h.sköldpadda har motsatta tecken i båda ekvationerna, vilka annuleras.
Den resulterande ekvationen blir:
2(h.bord)=300, från vilken vi kommer fram till h.bord=150
Visuell metod
Visuell metod: det andra sättet att lösa frågan är att tänka visuellt. Föreställ dig att du kan sammanfoga bilderna, så att basen på det första bordet (till vänster) sammanfaller med ytan på det andra (med andra ord, placera bilden till vänster ovanpå den högra).
Från denna nya figur kommer det vara möjligt att visuellt förstå att summan av höjderna 130 cm och 170 cm motsvarar exakt höjden på de två överlagrade borden, det vill säga 300 cm. Nu är det bara att dividera med två för att komma fram till höjden på bordet.
Kunde du lösa det? Vilken metod använde du?





