Ser du figuren som skiljer sig från de andra? Det finns en 3:a som är olik de andra

Om du har öppnat den här artikeln är det för att du gillar att testa dig själv, men framför allt din syn. För att lösa det här spelet och alla de som består i att hitta en figur som skiljer sig från många likadana, behöver du en bra syn, men den behöver inte vara med tio decimaler. Det behövs snarare en uppmärksam blick för att fånga de minimala skillnaderna mellan figurerna, i detta fall siffror, som alla ser likadana ut.
Kan du se figuren som skiljer sig från de andra?
Hitta den felvända 3:an
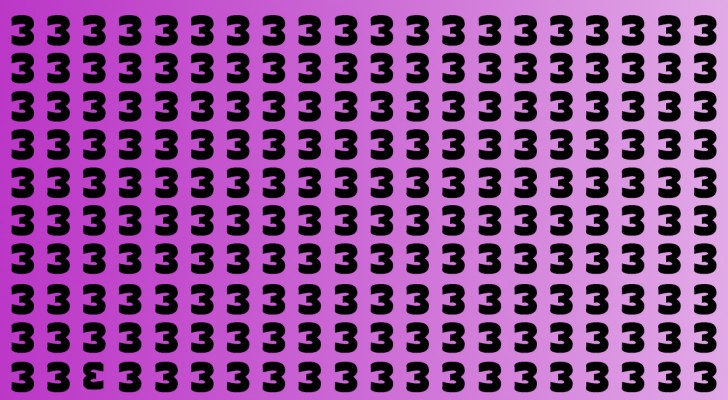
Curioctopus
Här får du en nästan oändlig sträng av siffran 3. I matematikens historia anses siffran 3 vara det perfekta talet. Men varför anses det vara ett "perfekt" tal?
Anledningen går tillbaka till Phytagoras, filosof och grekisk matematiker, som levde på 600-talet f.Kr. Han grundade Pythagoras skola och han var särskilt förtjust i siffran 3, till den grad att han betraktade den siffran som en perfektion. Anledningen är att tre representerar föreningen av en egenskap av siffrorna: Faktum är att 3 är summan av 2, jämnt tal och av delbarheten av 1, som inte är ett primtal. Därför är trean föreningen mellan jämna och udda.

Men låt oss gå tillbaka till spelet där du ska hitta 3:an som skiljer sig från de andra. Faktum är att på bilden, även om alla siffrorna ser likadana ut, finns det en som är olik de andra. Det är en bakvänd 3:a eller för att vara mer exakt spegelvänd vertikalt.
Det betyder att den annorlunda 3:an har "magarna" öppna åt det håll vi inte är vana att se på siffran 3. Denna lilla skillnad sätter hjärnan i svårigheter: kommer din blick att få syn på 3:an som skiljer sig från de andra?
Om du verkligen undrar var den finns och du har börjat misstänka att allt är ett skämt och att det verkligen inte finns en felvänd 3:a på bilden, avslöjar vi lösningen här: den bakvända 3:an finns och är placerad i sista raden. Kolla om du ser den nu när du har fått en liten ledtråd. Men om ledtråden inte är tillräcklig för dig får du hela lösningen här: den bakvända 3:an är placerad på sista raden, på tredje plats!
Nu när du har sett den är det uppenbart att den bakvända 3:an verkligen fanns bland de andra, eller hur?





